谷東応用未設定の制御担当です。
さて、ロボコンにおいて制御ロボにとって敵となるのは、「狙った角度に曲がること」ではないでしょうか。そこで今回は完璧に曲がる方法を数学を使って考えていきたいと思います。
※この記事は数学恐怖症の方には推奨しておりません。

今回は駆動部分だけを取り出し、簡略化して考えます。左右のタイヤの半径は r cm,横幅は t cm,そして肝心の速さを左右それぞれa°/s , b°/s とおいておきます。[図1]の中心にある黒丸はシャフトの中心を示します。
[図2]
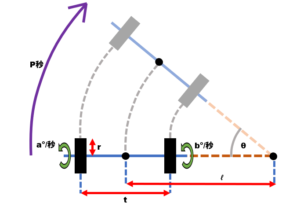
直進と回転運動は別々で考えます。回転運動は、[図2]のような場合を考えます。p秒かけてシャフトの中心から右に ℓ cm 右の点を中心としてθ°回転します。これでは左回転ができないようにも思えますが、左右反転させるだけなので問題ありません。直線運動に関しては、まっすぐ進むだけなので無視します。(一応 ℓ をとてつもなく大きい値にして θ を微小な値にすればできないこともないのだけれども)
[図3]

そして、便宜上各点を[図3]のように命名しておきます。移動前の左右タイヤ位置とシャフト中心をそれぞれ点 A , B , P、移動後はそれぞれ点 A’ , B’ , P’ とおき、中心は点 O とします。
準備ができたので早速計算していきましょう。
扇形 OPP’ の弧 PP’ の長さは、ℓ , θ を用いて
PP’ = 2πℓ × (θ/360) = πℓθ/180 ・・・①
と表せます。
また、a , b ,を扇形の相似に注目して用いると (相似の意味は興味があったら調べてみてください)
(ⅰ) OPP’ ∽ OBB’ より、
PP’:BB’ = ℓ:(ℓ – t/2)
ここで、BB’ = 2πr × (b/360) × p = πbpr/180
よって、PP’:(πbpr/180) = ℓ:(ℓ – t/2)
この比例式をPP’について解くと、PP’ = πbℓpr / (180ℓ – 90t) ・・・②
(ⅱ) 同様に、OPP’ ∽ OAA’ より、
PP’:AA’ = ℓ:(ℓ + t/2)
ここで、AA’ = 2πr × (a/360) × p = πapr/180
よって、PP’:(πapr/180) = ℓ:(ℓ + t/2)
この比例式をPP’について解くと、PP’ = πaℓpr / (180ℓ + 90t) ・・・③
①,②より、πℓθ/180 = πbℓpr / (180ℓ – 90t)
これをbについて解くと、b = θ/2pr × (2ℓ – t)
①,③より、πℓθ/180 = πaℓpr / (180ℓ + 90t)
これをaについて解くと、a = θ/2pr × (2ℓ + t)
これで公式ができました。
[図2]のような動作をさせたいときは、
左のタイヤは1秒当たり θ/2pr × (2ℓ + t) °
右のタイヤは1秒当たり θ/2pr × (2ℓ – t) ° 回せばよい。
ただし、モーターの性能が左右で違う場合、この公式は役に立ちません。
つまり、ほとんどの場合、この公式は意味がありません。
(サーボモーターはたぶん大丈夫ですよ)
以上



コメント